√99以上 片対数グラフ 傾き 最小二乗法 261988-片対数グラフ 傾き 最小二乗法
血中濃度データに経口投与モデルを当てはめる 薬剤師のプログラミング学習日記
誤差を二乗する 最小 二乗 法という言葉には「 二乗 」という文字が入っていますが、これは 誤差を二乗する操作 がこの方法のキーポイントだからです。 誤差の二乗とはつまり式 (2)です。 この後、各データポイント毎の誤差の総和をとった数値を最小化するわけですが、二乗することで誤差が全て正の値になるようにすることができます。 最小化する対象に負の値があると、近似した R = 1987, V 0 = と求まり、直線の傾き R および切片 V 0 を求めることができます。 これが、最小2乗法の使い方の例です。 実は実験の後、教授から「この抵抗、本当は2 Ωなんだよ～」と教えてくれました。 このように、実際の値かどうかはわからないが、表向きに言われている値のことを 公称値 とよびます *4 。 2 Ωだといわれている抵抗に対して、1987 Ω (相対誤差
片対数グラフ 傾き 最小二乗法
片対数グラフ 傾き 最小二乗法-21 グラフに表す方法 2つの量を両軸に取り、測定値を表す点を方眼紙にプロットする。 そしてそれらの点の関係を最もよく適合する直線や曲線を引く。 縦軸と横軸の目盛りの取り方であるが、理想的には、測定値の有効数字の最後の桁の1が方眼紙の1目 最小二乗法とは、予測値に基づくy=axbの回帰直線上の値と、実際の値との差の2乗が最小となるような回帰直線を求める方法です。 エクセルで最小二乗法の傾き (a)と切片 (b)を求める方法の1つがLINEST関数を使う方法です。 そのほかエクセルの分析ツールを
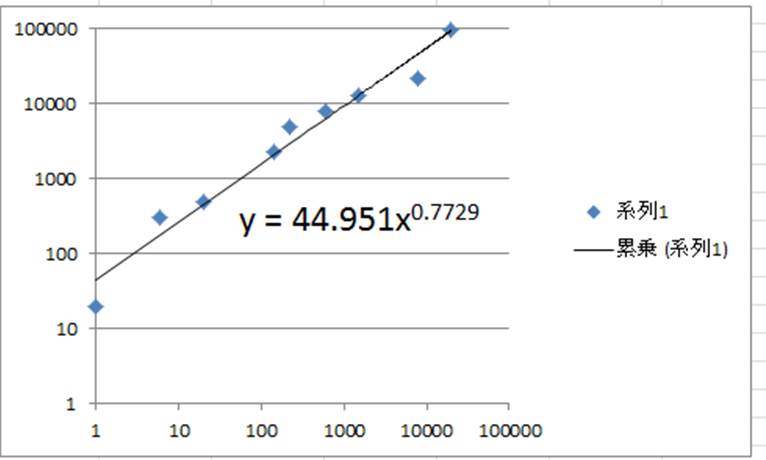
Excel エクセルで両対数グラフを作成する方法 両対数の傾きの意味は
どちらの方法も、グラフの傾きと切片を求めるのに重要であるため、きちんと理解しておきましょう。 まとめ ここでは、エクセルで回帰直線の傾きと切片を計算する方法について解説しました。 第一の方法として、データを実際にグラフ化し、そのプロットに対する数式付きの近似直線をYを対数に、片対数グラフ用紙にプロットすると直線になる。 他の関数の場合と同様に、A,Bを決定する。次に述べる最小二乗法で求めても良い。 24 最小二乗法により2つの量の関係式を求める方法について 前掲の出力電流Iと変位xのデータの関係が例えば，累乗近似式は両対数グラフで線形となるように変数変換している。 対数部分を以下のように置換してみると良く分かると思う。 このように変換された変数に対して最小二乗法を適用しているので，当然，元のデータに対する回帰式とは異なる。 同様に，指数近似も片対数変換して線形
エクセル近似曲線の「指数近似」「累乗近似」は、いわゆる非線形最小二乗法ではない。 ・エクセルで用いているのは、データの対数に直線をあてはめるという方法。 ・いわゆる非線形最小二乗法とは、残差（誤差）の2乗和を最小にする方法。 詳しいことは以下のページで尽きているのだ 片対数グラフの傾きについて 0005 現在，片対数グラフ(横軸を対数表示)を用いて，金属疲労に関するsn線図(ウ゛ェーラー線図)を数式表示しています。しかし，その際に，次の式を用いるのですが， σ＝c・n^(k) 私の場合，sn線図は全部で4本あります。一枚の片対数グラフに2本ずつ存在 指数関数の意味。 高校生からわかる近似曲線に指数関数を選ぶとき こんにちは ( @t_kun_kamakiri )。 2つの量x x とy y の関係性を調べるのに、グラフにデータをプロットしていきその関係性を視覚的に見たりしますよね？ 1次関数で近似したり、2次関数で近似
片対数グラフ 傾き 最小二乗法のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
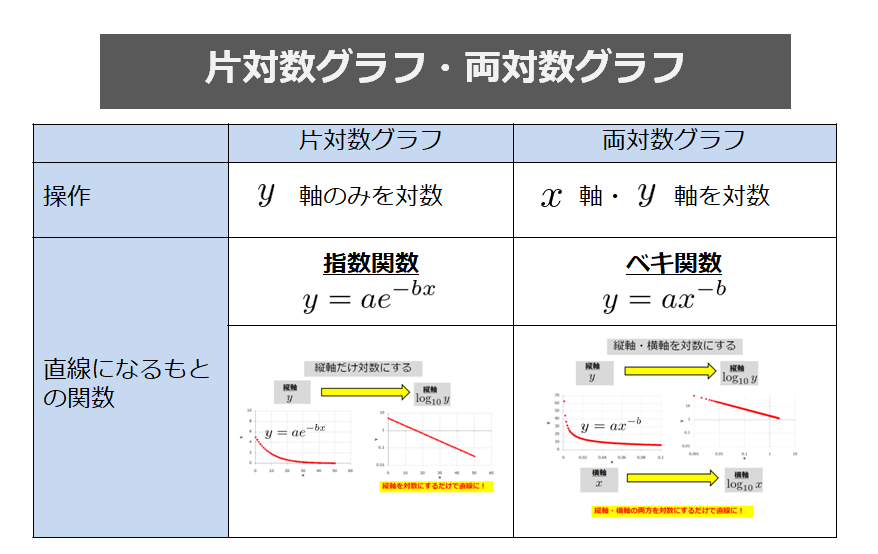 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg | 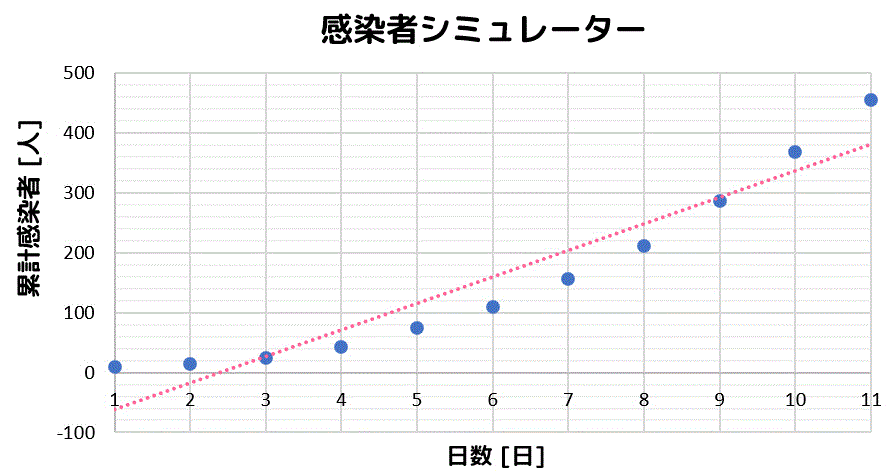 Image4 Jpg |
Image4 Jpg | 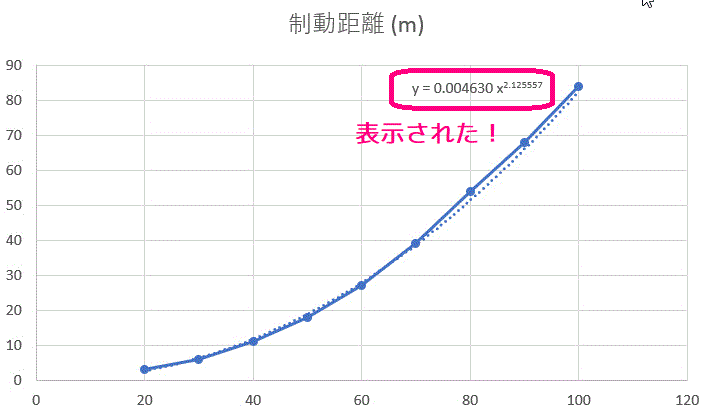 Image4 Jpg |  Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg | Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 Image4 Jpg |  Image4 Jpg | Image4 Jpg |
 Image4 Jpg |  Image4 Jpg | Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 Image4 Jpg |  Image4 Jpg | Image4 Jpg |
 Image4 Jpg |  Image4 Jpg | Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg | Image4 Jpg |
Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
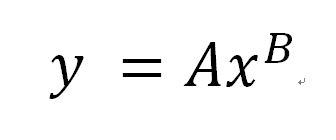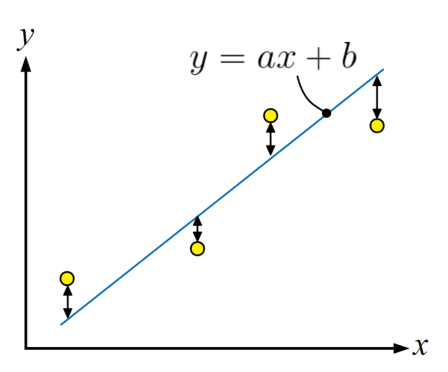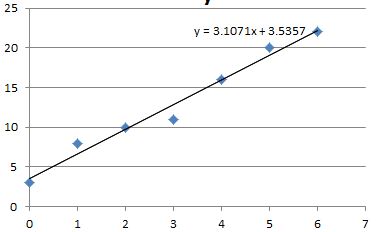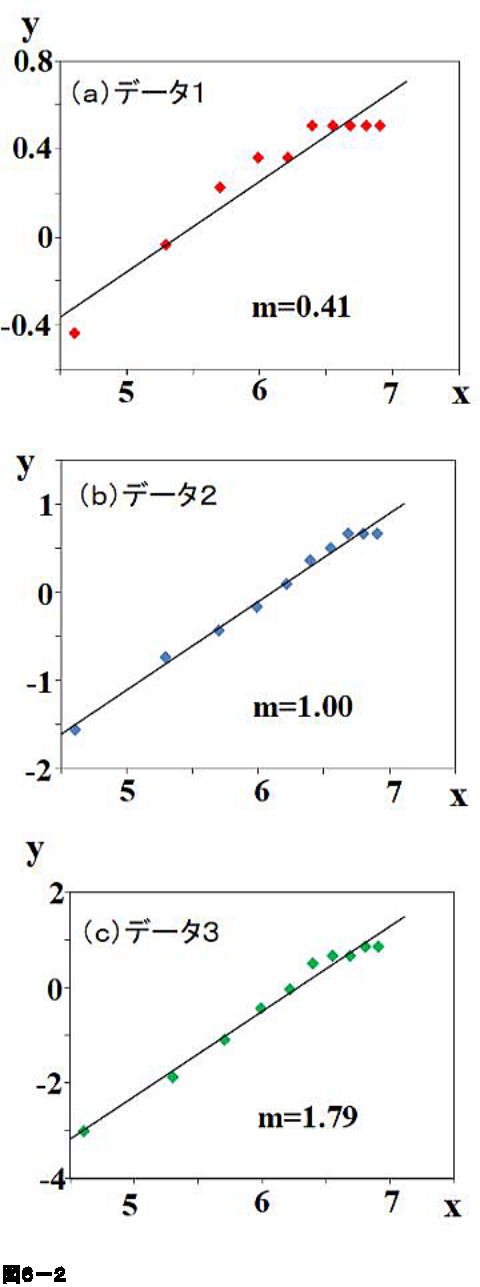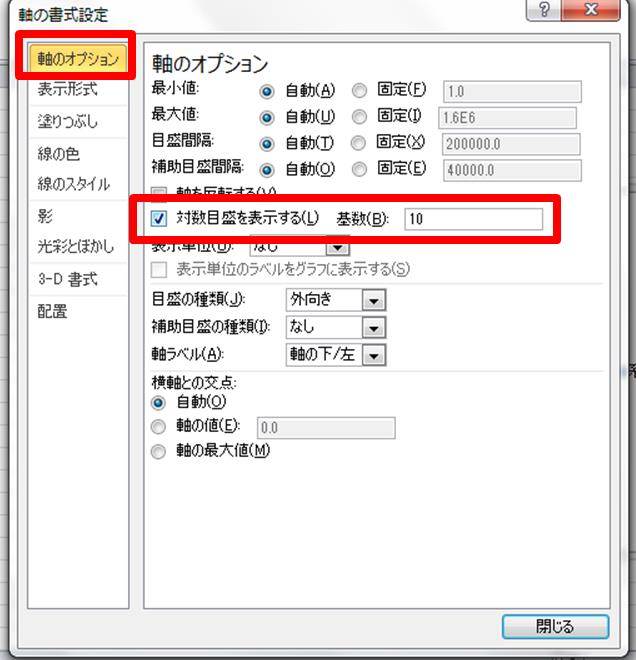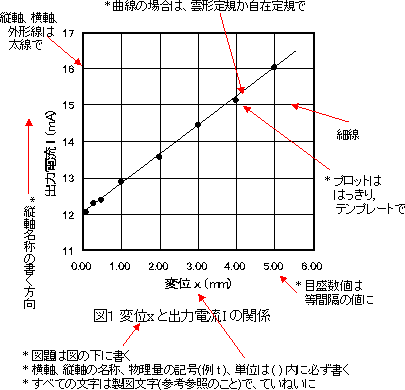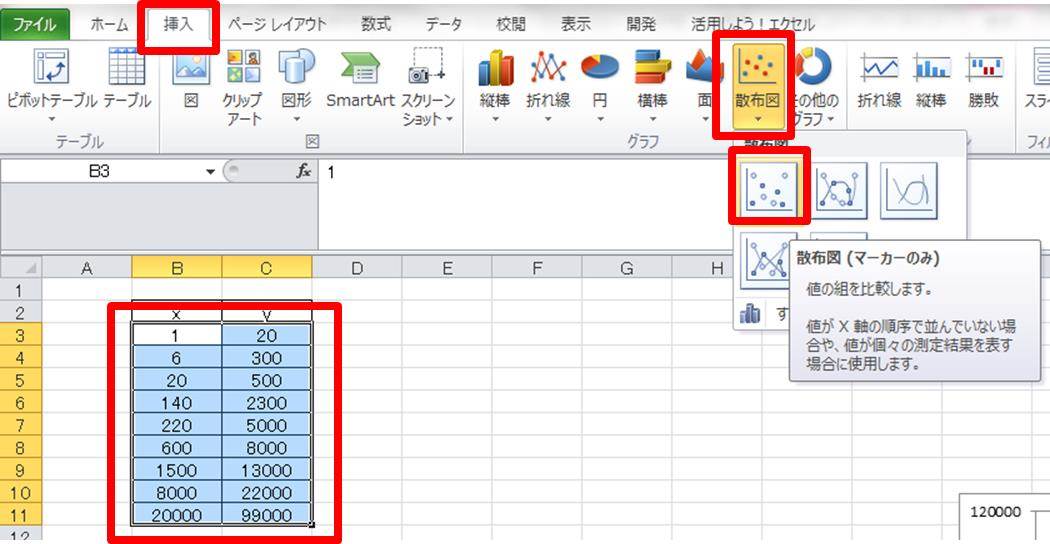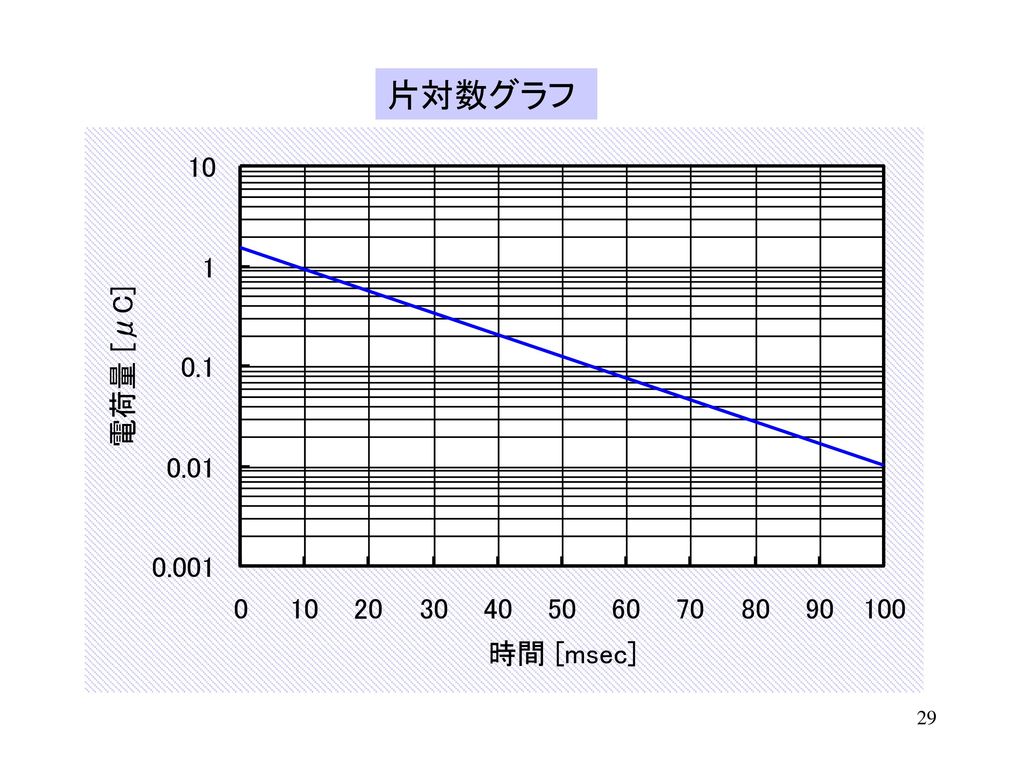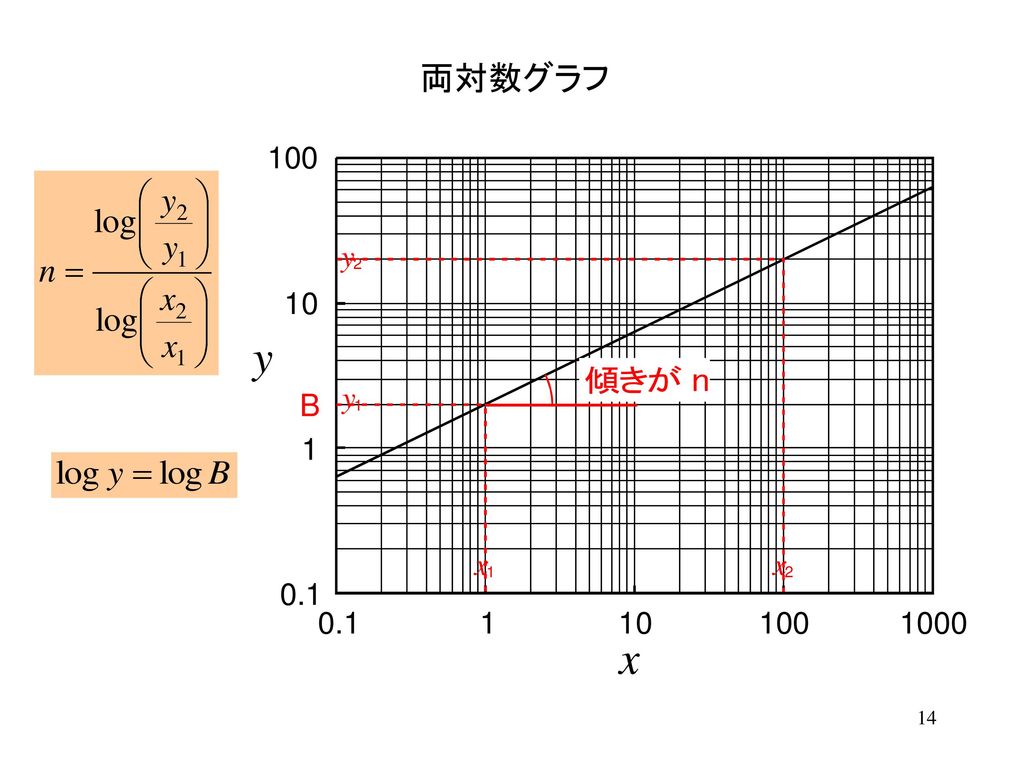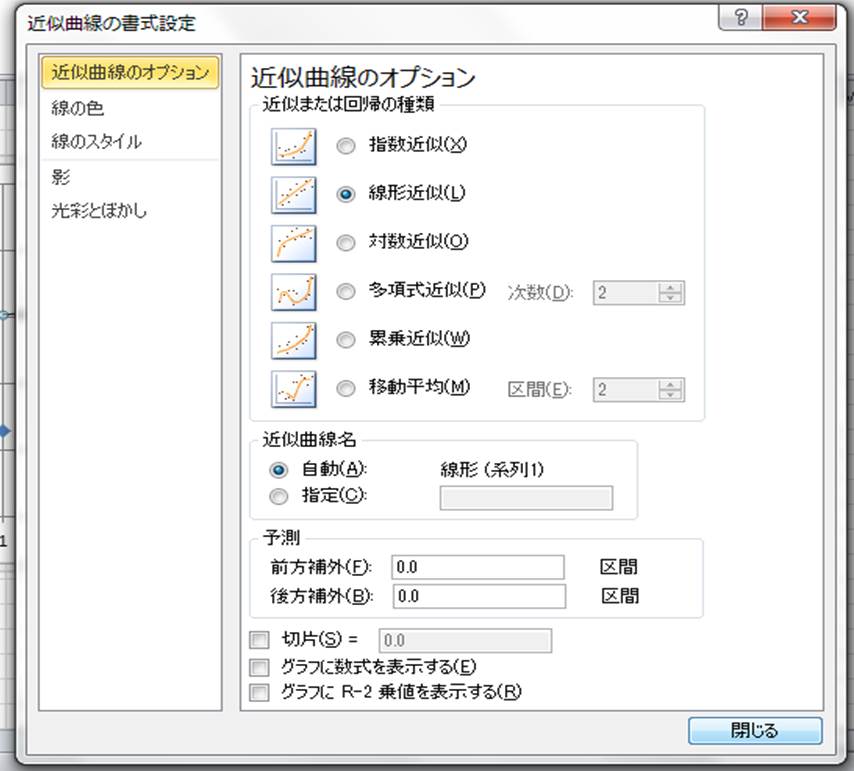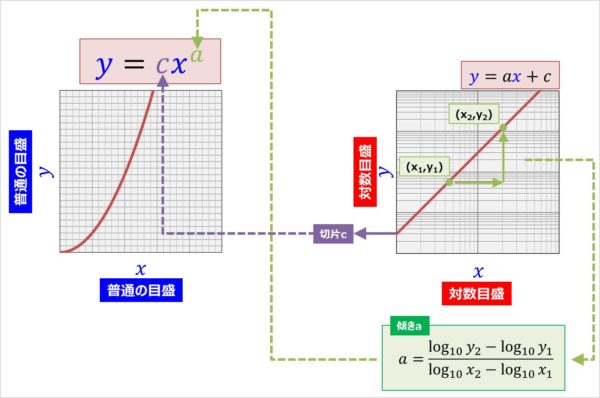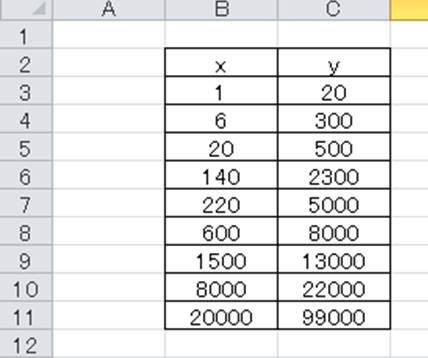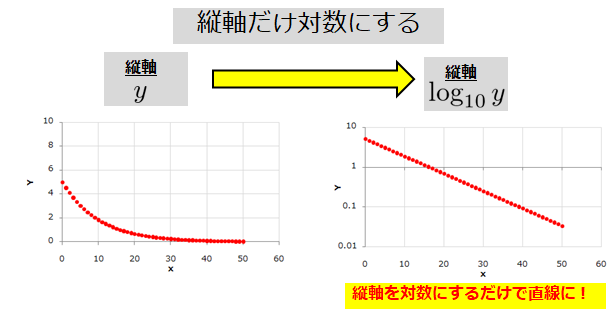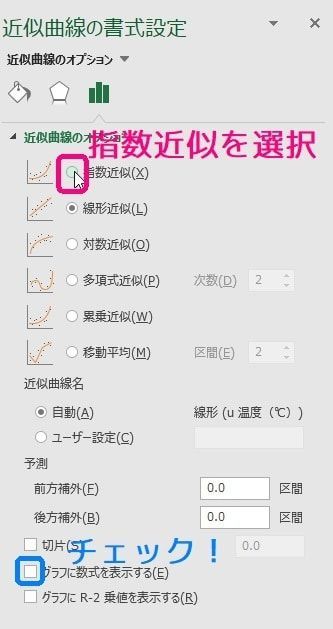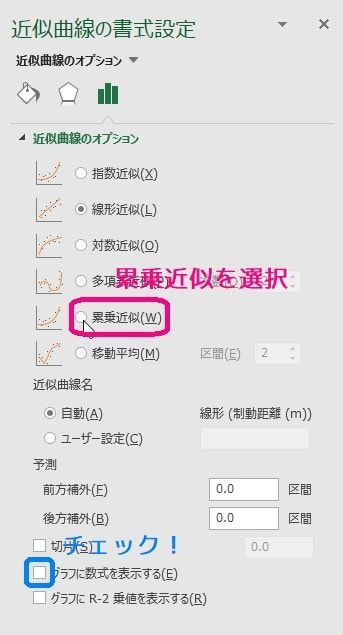 Image4 Jpg | Image4 Jpg |  Image4 Jpg |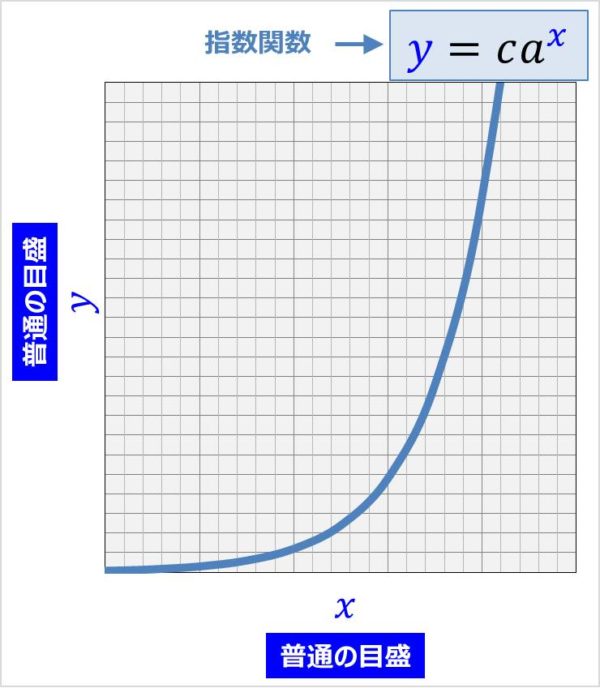
 Image4 Jpg | 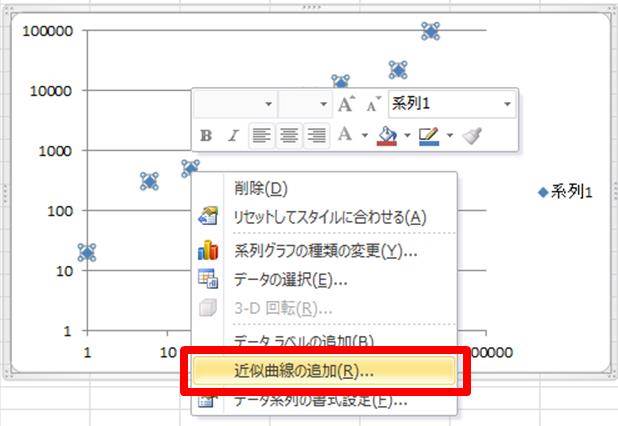 Image4 Jpg | 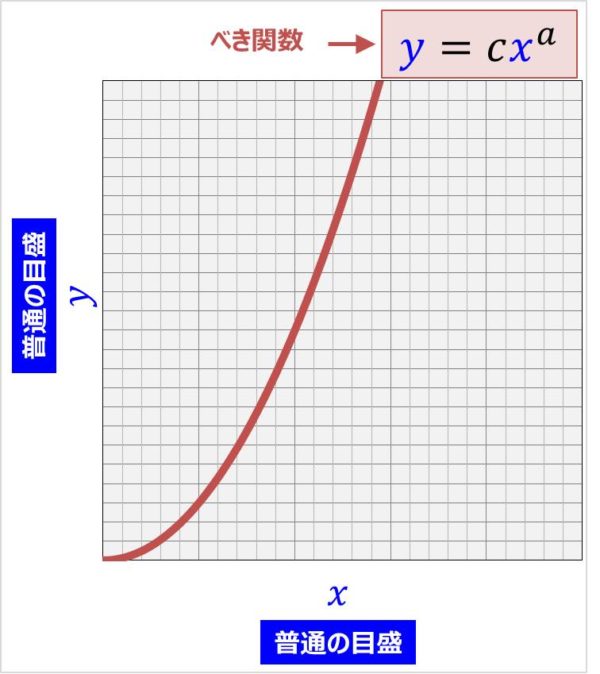 Image4 Jpg |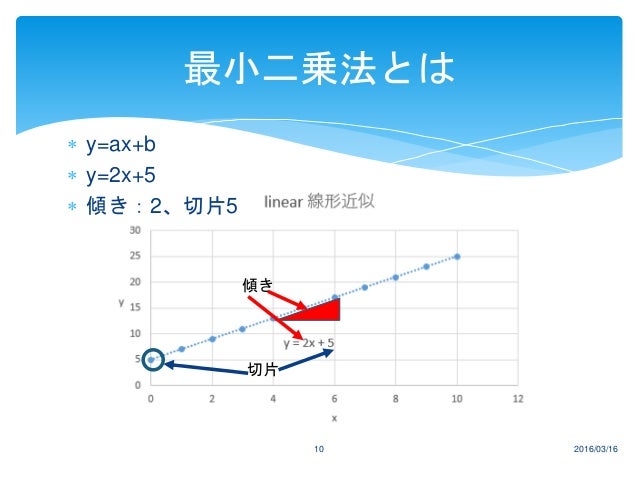
 Image4 Jpg |  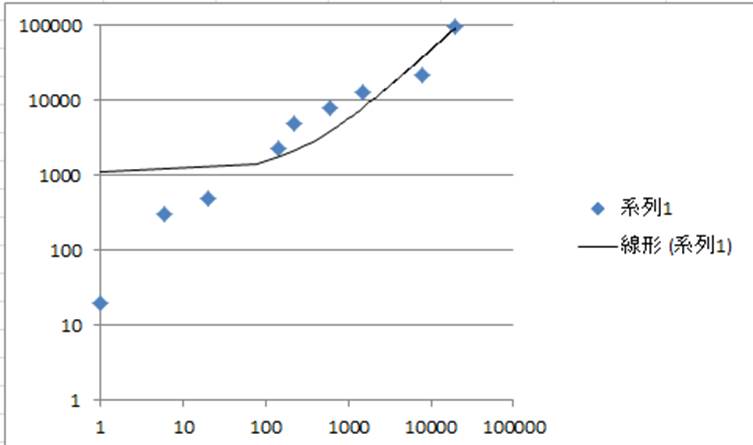Image4 Jpg | Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 Image4 Jpg | 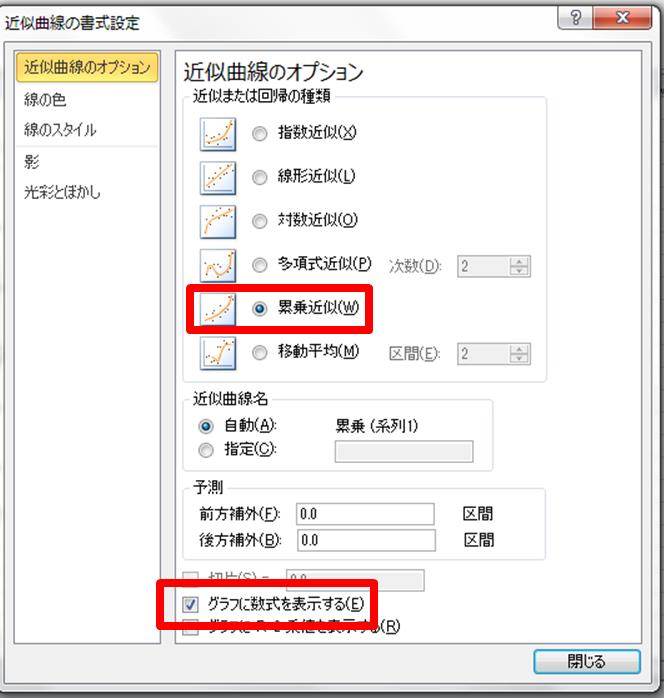 Image4 Jpg |  Image4 Jpg |
 Image4 Jpg |  Image4 Jpg |  Image4 Jpg |
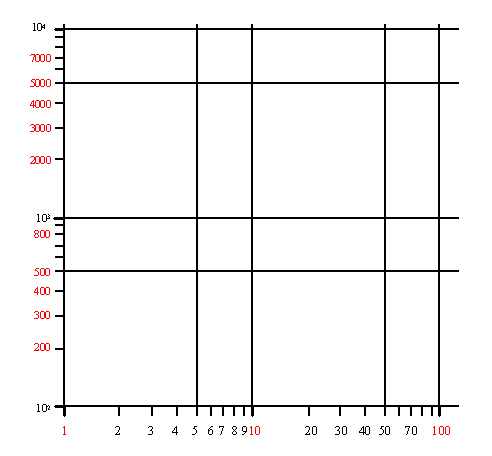 Image4 Jpg | 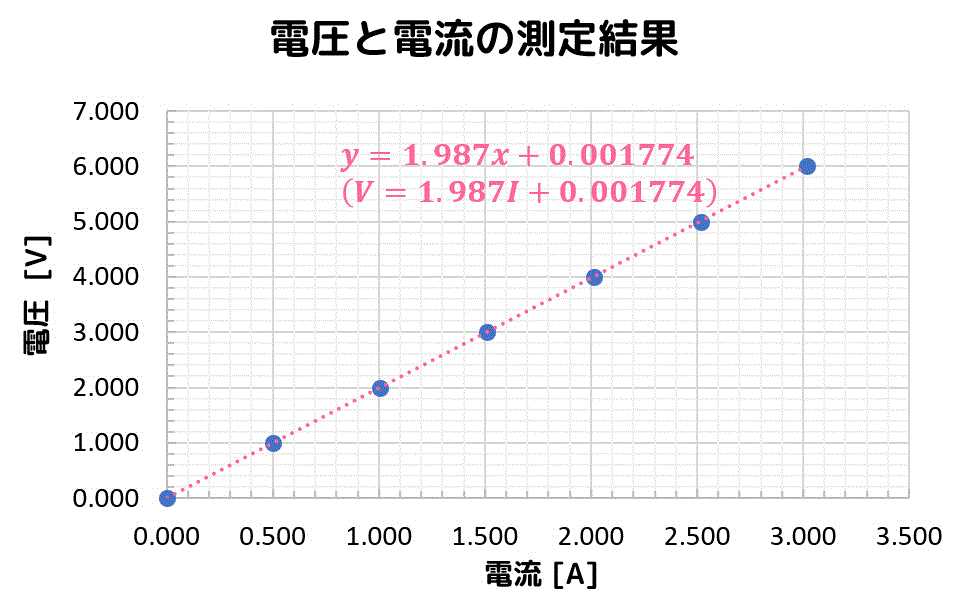 Image4 Jpg | 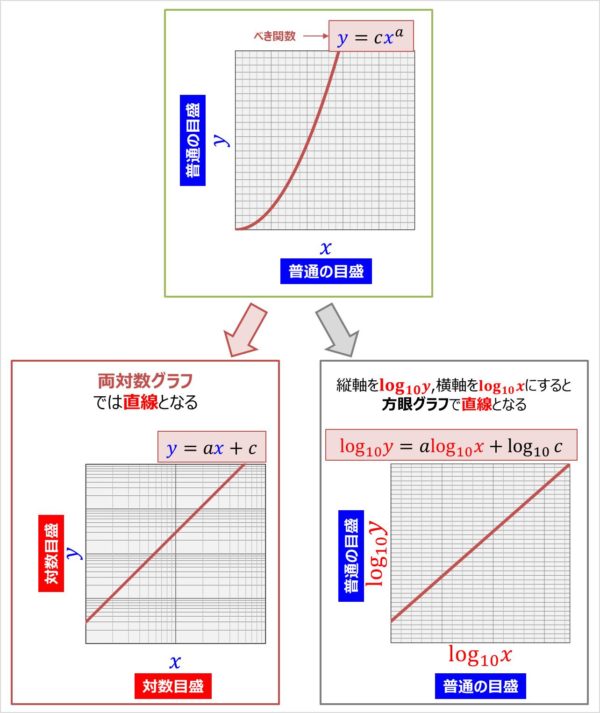 Image4 Jpg |
「片対数グラフ 傾き 最小二乗法」の画像ギャラリー、詳細は各画像をクリックしてください。
 Image4 Jpg |  Image4 Jpg | 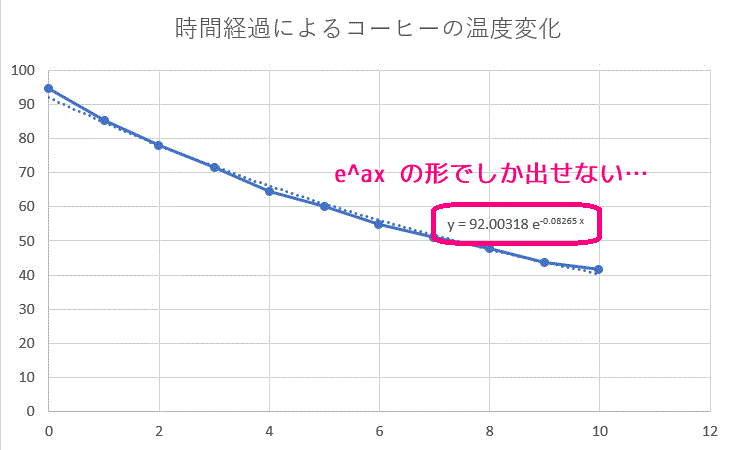 Image4 Jpg |
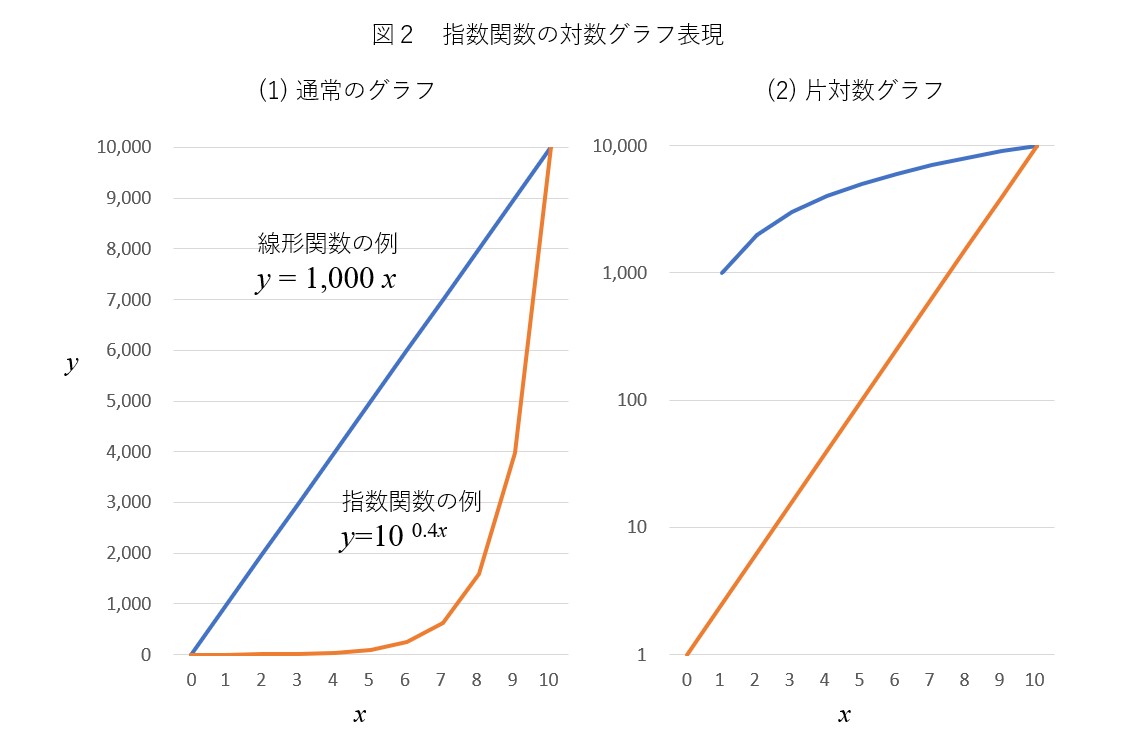 Image4 Jpg |
ここのところ、Excelの多項式近似で悩んでいた件のメモ。 例えば、下記サンプルデータとグラフが有るとします。 グラフ上で右クリック → 近似曲線の追加で下記のように設定すると 近似式とR2の値が表示されます。 このR2の値（）が欲しいのですが、その都度Excelを立ち上げ最小2乗法は、測定点における直線との差の2乗を最小にするような直線 (axb)の傾き (a)と切片 (b)を求める方法である。 原理は各自理解しておくこと。 (参考文献 「物理化学実験法」、鮫島実三郎著、裳華房、p 12) 解析を行うのに便利な関数として他に、sum
Incoming Term: 片対数グラフ 傾き 最小二乗法,
コメント
コメントを投稿